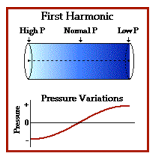
In the simplest or the fundamental mode of vibration in an open pipe, the air column vibrates in the pattern shown to the left. This represents only 1/2 of the wavelength of that particular sound.

In an open pipe, when a compressed wave reaches the far end, the air at that point is, for an instant, at a pressure greater than the atmospheric pressure. Being an open end, the air there can vibrate with maximum freedom and so, it suddenly expands into the surrounding air. Thus, the pressure diminishes so quickly that it becomes lesser than the pressure of the surrounding air, which causes a sudden rarefaction at the end of the pipe. This sets up a rarefied wave which passes back along the pipe. Within the tube, the reflected pulses meet the direct ones and the result is the formation of the standing waves of length 2L, where L is the length of the pipe.

Frequency of the sound (in Hz, or cycles/second) is equal to the velocity of sound (1125 feet/sec) divided by the wavelength or f=V/Wavelength or f=V/2L. Thus the fundamental frequency of an 8' open pipe would be 1125/16 which is about 70 Hz, close to the 64 Hz we have been using for the low C of an 8' open pipe.

If the pipe were closed at the end, the formula would be f=V/4L so an 8' closed pipe would generate a sound of about 35 Hz.